Jan 28, 2021
https://astralcodexten.substack.com/p/ontology-of-psychiatric-conditions
[reposted from here, with edits]
I.
Taxometrics is the study of whether psychiatric conditions are categorical or dimensional.
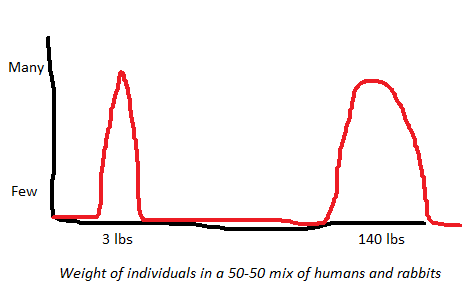
Something is categorical if it neatly, objectively separates into different groups. For example, consider humans and rabbits. If we take a mixed group containing some humans and some rabbits, and graph them along some variable like weight, it would probably look like this:
There’s one big obvious group around 3 lbs (weight of the average rabbit) and another around 140 lbs (weight of the average human). Not a lot of subtletly here. If we used some other graphable variable – height, lifespan, IQ – we’d probably get something similar.
Maybe the biggest rabbit in the world is bigger than the smallest human. That doesn’t mean they’re not two obvious categories. It just means they’re two obvious categories with a tiny overlap. It happens.
If we wanted to be clever, we could create a multivariate distance measure that combines weight, height, lifespan, IQ, and lots of other ways humans and rabbits could differ, into a 0 – 1 variable where 0 is “most rabbity” and 1 is “most humanish”. Probably these scores wouldn’t overlap at all – if they did, it would mean there’s some human who’s more like a rabbit than some rabbit is, which would be pretty surprising. But even if this were true, it wouldn’t change the fundamental finding that humans and rabbits are pretty different. Or to put it some other way, there’s a fundamental hidden generator producing differences between humans and rabbits (in this case, the species difference).
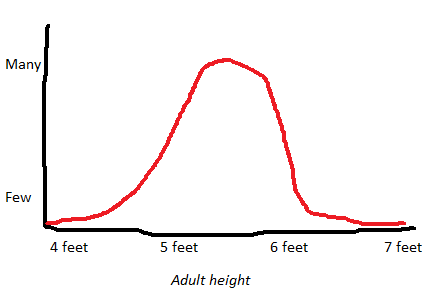
By contrast, something is dimensional if it’s just a spectrum and there’s no obvious place to separate it into different groups. For example, consider tall people vs. short people. We take a general cross-section of the population, and graph them by height, and it would probably look like this:
There’s no clear point where short people stop and tall people begin. Some people are a little taller than others, and other people taller still, and so on until you’re at Yao Ming.